On shallow estuaries, tidal calculations are vital, but Ken Endean finds errors in online predictions

Tidal calculations can be tricky. Sometimes back-to-basics is best – certainly don’t believe everything you find on the web.
For pilotage in shoal waters a sailor needs to know the depth, which depends upon the height of tide.
To calculate height of tide for times between high and low water, the conventional method involves a pencil-and-paper exercise, working from tidal curves published in almanacs, or often these days, the number is plucked straight from a phone app, often based on generic tidal curves.
However, in shallow estuaries the banks impede the flow of water, distorting those tidal curves.
Inaccurate or overly simplified tidal curves can lead to dangerous inaccuracies in your expected depth.

Tidal calculations: At Granville, the foreshore dries for a long way out but the marina has a sill to retain water. Credit: Ken Endean
On countless rivers around our coast, you wouldn’t want to arrive at the rivermouth bar only to be driven aground because you’re an hour too early, or too late.
The same is true for marinas and harbours protected by locks and sills.
A full analysis requires intricate maths, usually on a computer, but some computerised output of tidal calculations on websites contains gross errors.
In those cases, using a pencil to sketch adjustments to the almanac’s tidal curve can actually yield more accurate results.
For this it is vital that the skipper should have a good mental picture of what happens when the sea flows into and out of the estuary.
Tidal calculations: Tidal sills
One obvious way in which a shallow estuary can interfere with the flow is by a natural sill, such as a drying bar.
To illustrate general principles, I’ll start with a simple example of a man-made tidal sill.
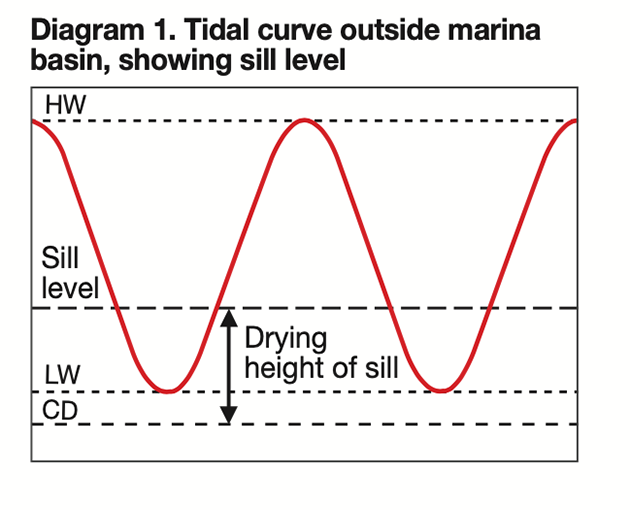
Diagram 1 (below) shows a typical set of tidal curves (with time and height scales omitted).
Credit: Maxine Heath
A marina basin has water retained by a sill and the drying height of the sill is marked on the graph.
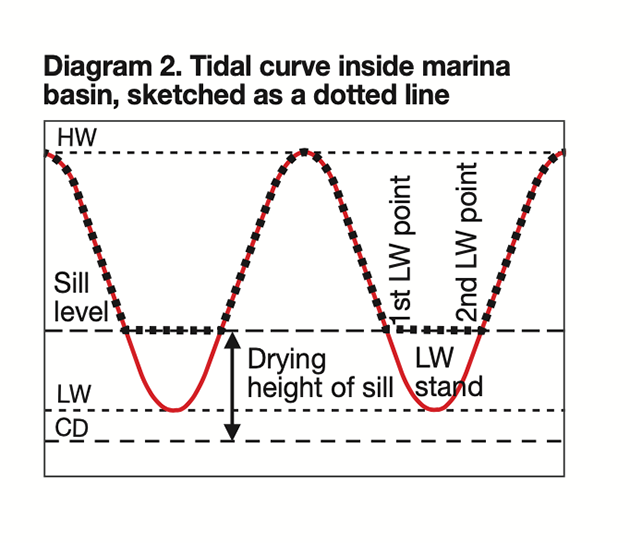
The water level in the basin cannot fall below the sill level, so we can create a tidal curve for the interior of the basin by sketching on a hand-drawn line, as indicated by the dotted line in Diagram 2 (below).
Credit: Maxine Heath
In essence, we have chopped off the bottom of each tidal curve and after each high water we now have two low water points, with a low water stand between them.
A similar curve can be drawn for a place on a drying estuary, but this is where some computers get confused.
Tide predictions are generally based on harmonic motions, as if the height of tide is bouncing up and down smoothly between high and low water points, but where a sill creates two low water points the first will be a dead bounce, with no upward turn until the second low water point, when the next flood over-tops the sill.
Some prediction programs can’t handle that and when they ignore either the first or the second low water the result can be dangerously inaccurate.
Chart datum: fixed or variable?
To check a prediction by hand we first need to know the drying height.
In some estuaries the charts display all drying heights in relation to the coastal chart datum, while in others the chart datum is stepped up to follow the rise in the drying channel as it winds inland.

Much of the Fowey Estuary dries, and a chart diagram shows the steps in the chart datum. Credit: Alamy
For a few places, including the Fowey River and the Gulf of Morbihan, the charts have diagrams of the datum steps.
Many estuary charts have datum steps that are not mentioned in the chart notes, and we have to deduce the relevant measurements from the tidal data in almanacs.
The first clue lies in the height of mean high water springs (MHWS), which is measured above chart datum.
On a short estuary, at high tide the water surface will be approximately flat and level from the mouth to the tidal limit.

The author’s boat, London Apprentice, happily dried out up the Fowey Estuary. Credit: Ken Endean
If there is a single, level chart datum the height of MHWS will be constant throughout the estuary, and where the bed is above the chart datum it will be marked with a drying height.
However, if the chart datum steps up, the almanac’s data block may indicate the height of MHWS at inland locations is less than at the mouth
Case Study: Wells, Norfolk

Tidal calculations: Wells approach channel dries almost completely. Credit: Ken Endean
Wells, in Norfolk, is a good example of a potentially hazardous estuary.
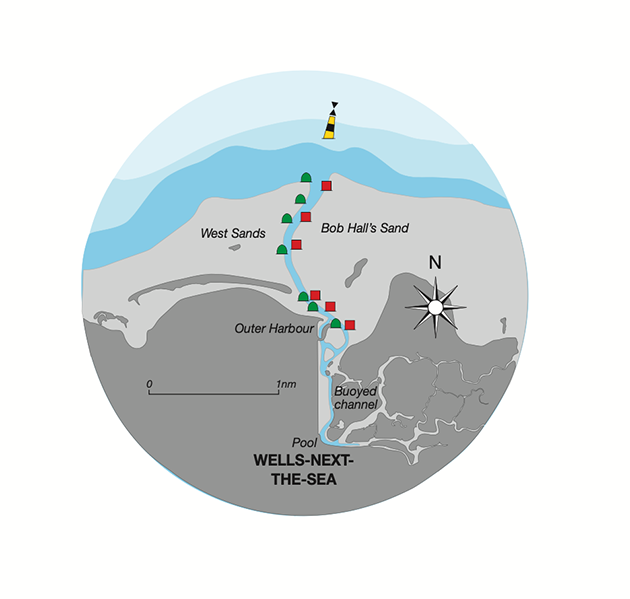
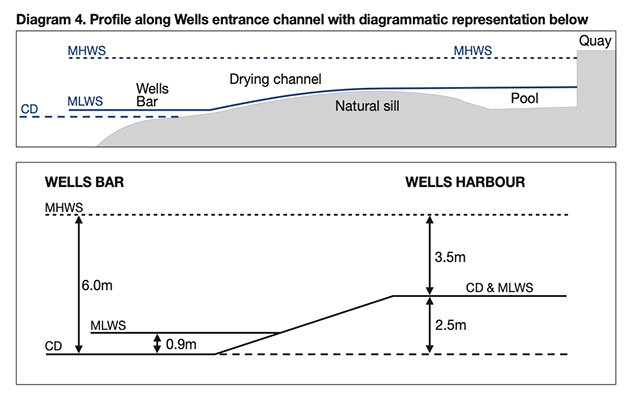
Diagram 3 (below) shows a plan of the entrance channel, which dries for most of its length, and Diagram 4 (below) is a longitudinal profile.
Credit: Maxine Heath
North Sea swell often breaks as it runs over the outer sands, at the point known as Wells Bar, but the shallowest part of the entrance is further inshore, where the drying channel acts as a natural sill, retaining a low-tide pool by the town quay.
Credit: Maxine Heath
For this inner harbour, a hand-drawn tidal curve can be produced as follows. (NB. In this example I have used figures for mean spring tides.)
- Identify the tidal parameters for the mouth of the estuary: Diagram 5 (below) shows a tidal curve for Wells Bar, based on the standard port of Immingham, and the usual data block with height and time differences from Immingham.
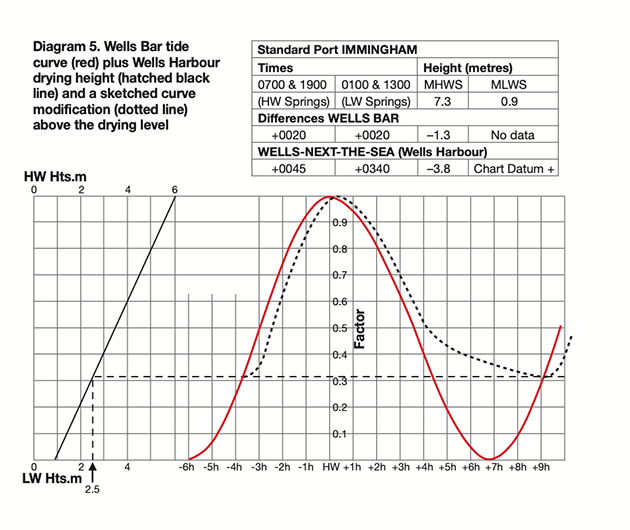
Credit: Maxine Heath
The red curve has been extended to include the start of the next flood. Using the height differences, the height of MHWS at Wells Bar will be: MHWS Immingham minus the difference for Wells Bar: 7.3 – 1.3 = 6.0m. As there is no data for MLWS at Wells Bar,
I have assumed 0.9m, which is the value at the nearby coastal tidal stations of Cromer and Hunstanton. In the left-hand part of the diagram, those figures of 6.0m and 0.9m have been used to draw the usual diagonal line that relates tidal heights to the tidal curve.
2. Work out the drying height of the channel: From the height differences again, MHWS in Wells Harbour is 7.3 – 3.8 = 3.5m. That is 2.5m less than MHWS at the bar and indicates that the chart datum has been stepped up by 2.5m, to the height of the natural sill, as shown in Diagram 4. On the left-hand part of Diagram 5, I have inserted a vertical hatched line at a tide height of 2.5m, and from where it meets the diagonal it carries on horizontally across the diagram, chopping through the lower parts of the tidal curve.
3. Sketch in a modified tidal curve: Now comes the artistic bit. Wells Harbour with its many creeks takes longer to fill than a marina basin and the data block shows that high water in the harbour is 25 minutes later than on the bar, so I have sketched in a freehand curve, shown as a dotted line, starting from where the red line of the rising tide overtops the hatched line from the level of the natural sill, but following 25 minutes later than the red line. It won’t be exact but is a reasonable approximation. On the ebb side of the curve, it continues down, 25 minutes behind the red line, but as it approaches the natural sill level I have made it level off before it reaches the first low water point, because the late outflow will decrease as water drains out of the creeks.
What about the web?
For comparison with my hand-drawn estimate, Diagram 6 (below) adds curves taken from websites.
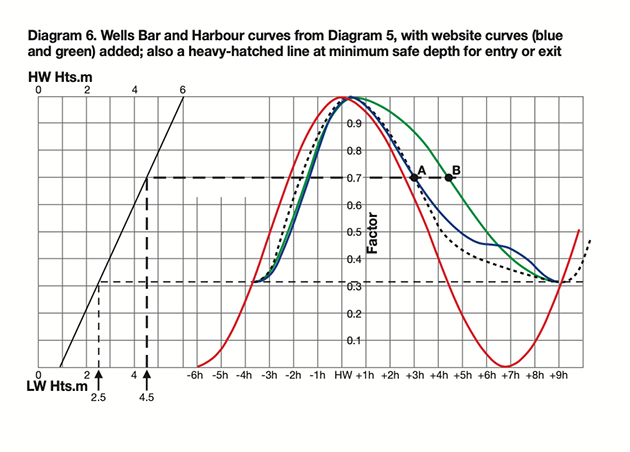
Credit: Maxine Heath
The blue curve is from the UKHO’s Easytide predictor, and it is very close to my sketched curve.
However, the green line has been taken from a website (which I won’t identify) and is a gross simplification that ignores the first low water point and runs in a smooth curve directly to the second low water point.
This could have serious consequences for a yacht entering or leaving during the ebb. If she needs, say, 2m depth over the shallows, which dry by 2.5m, that will require a tide height of 2.5m + 2m = 4.5m above the chart datum at the bar (on this diagram I have inserted a second height-of-tide line corresponding to that level).
Both my sketched curve and the Easytide curve cut this heavy-hatched line at Point A, three hours after HW on the bar (2h 35m after HW in the harbour), suggesting that arrival or departure should be possible until this time, which is consistent with the harbour authority’s normal guidance.
However, the website suggests that entry and exit will be safe until the green curve meets the hatched line at point B, 4.5 hours after HW on the bar.
In fact, anyone attempting to enter or leave at that time is likely to hit the sand, which could be catastrophic.
Long, shoaling channels

Barnstaple Quay dries, so when can you arrive or depart? Credit: Ken Endean
At a short estuary such as Wells, the tide simply flows in, pauses with the harbour full, and then flows out again.
However, in a long, shoaling estuary the tide behaves partly as a wave (of which the Severn Bore is a famous example), with its speed dropping as the depth decreases.
The leading edge of the wave is in the shallowest depths and is slowed down so that the crest catches up, resulting in a short duration of flood with a rapid rise, as illustrated in Diagram 7 (below).
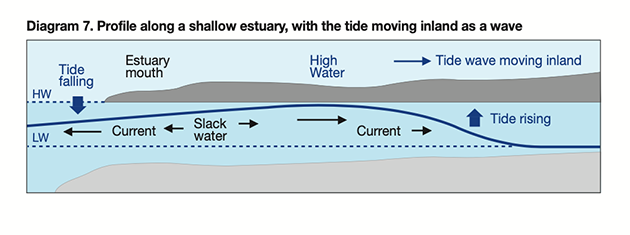
Credit: Maxine Heath
Diagram 8 is a chartlet of the Taw/Torridge estuary in North Devon and Diagram 9 shows relevant tidal curves and almanac data block.
The solid red line and the diagonal height line are for Appledore, near the mouth, where MHWS is 7.0 + 0.5 = 7.5m. Barnstaple is 7 miles upstream on the River Taw, where the MHWS is 7.0 – 2.9 = 4.1m, suggesting that the channel has a drying height of 7.5 – 4.1 = 3.4m, indicated by the hatched black line.
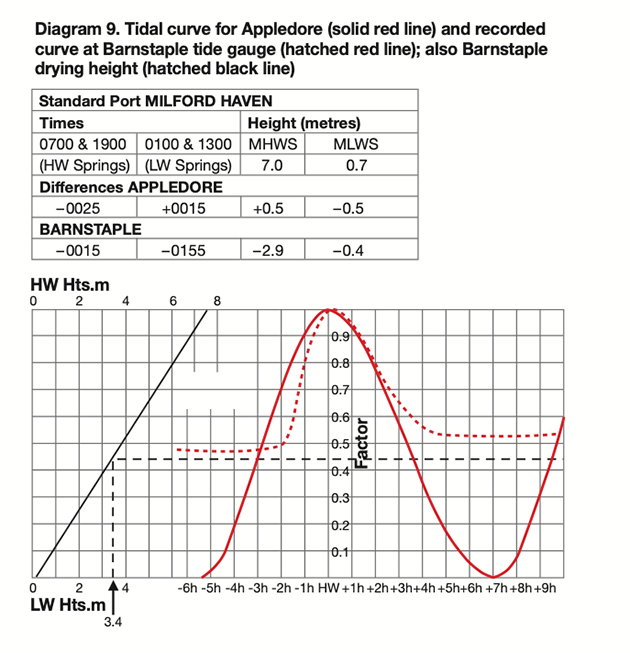
Credit: Maxine Heath
(NB. the principal Admiralty chart has a data block that provides similar figures more directly, but that information is not available on all charts, so I have worked this example from the almanac.)
Just as I did at Wells, I could sketch in a curve for Barnstaple but here we have something better: the hatched red line uses factual data from the tide gauge at Barnstaple Quay.
On the rising curve, it resembles the hand-drawn curve for Wells, but with a greater initial delay and a steeper rise, although after high water the ebb curve starts to drop promptly.
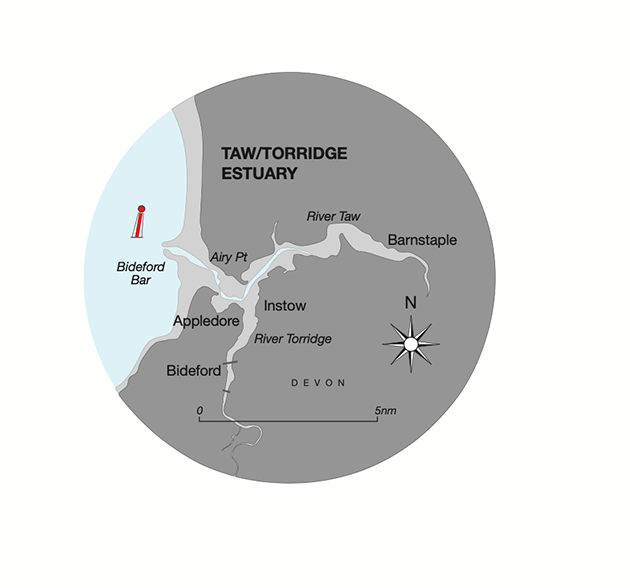
Diagram 8. Taw/Torridge Estuary. Credit: Maxine Heath
That is because the Taw’s tidal limit is several miles upstream of Barnstaple and the tide wave rolls on beyond the town, with the level dropping quickly after
the crest has passed. As we would expect, there is a lengthy stand over each low water period.
The tide gauge recorded the second low water period at a higher level because heavy rain had generated more fresh water flow.
As the tide gauge output is gospel rather than guesstimate, we can use it confidently to test the accuracy of website tidal curves, and here the UKHO’s Easytide programme reveals its limitations.
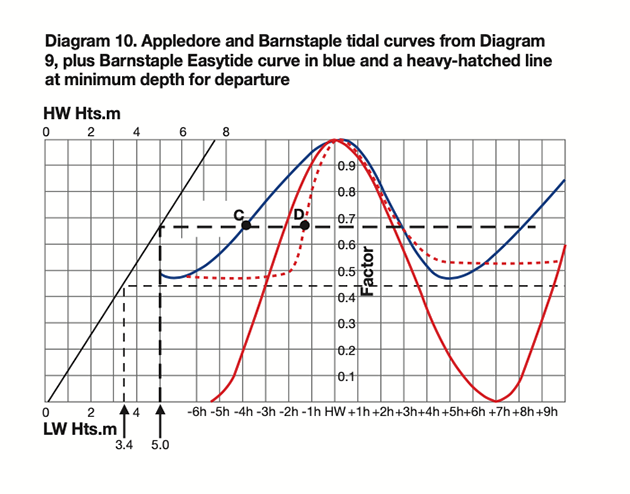
Diagram 10 (below) shows the Easytide curve superimposed on the curves from Diagram 9, and it’s clear that the programme has ignored each second low water point, running the curve directly from the first low water point to next high water.
Credit: Maxine Heath
As at Wells, simplification creates risks.
If a boat is to leave Barnstaple Quay on the flood and head out to sea, let’s assume that she can float and move when the depth reaches 1.6m, which will be at 3.4m + 1.6m = 5.0m above the chart datum at Appledore.
On the diagram, I have inserted a heavy hatched line for that height of tide. Easytide’s blue curve meets that line at Point C, about 4 hours before high water, and that, if true, would allow ample time to get down the river.
However, in real life the boat will be aground until the tide gauge’s curve meets the heavy hatched line at Point D – less than 1½ hours before high water.
If it departs at that time, it will not clear the estuary until after high water, which could be dangerous because Bideford Bar has a reputation for heavy breakers on the ebb.
It might be sensible to anchor off Appledore, then depart from the river on a later tide. That will probably add a day to the passage plan and the skipper will be distinctly unimpressed by the Easytide curve.
The Easytide website actually carries a precautionary warning: ‘Easytide must not be used by vessels for navigation’.
Some other websites have suspect curves but no such warnings. Why publish an inaccurate tidal curve?
Timing of flood streams

Tidal calculations: Pilotage in the upper Severn Estuary demands very through preparation. Credit: Ken Endean
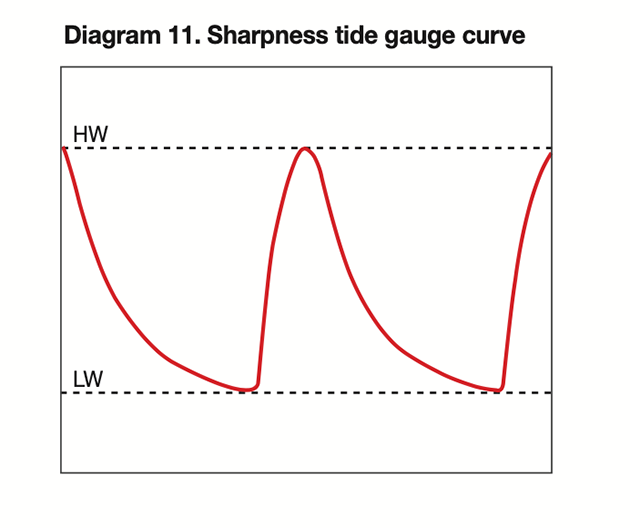
Shoals can play other tricks with the flow of water. Diagram 11 (below) shows a curve plotted from the tide gauge at Sharpness Harbour, in the upper Severn Estuary.
The mighty Severn flood is slowed by the extensive sand banks and when it arrives it does so in a surge, with the water level rising fast enough to be followed by eye.
Credit: Maxine Heath
An up-river passage plan must anticipate that there will be little rise until a couple of hours before high water, when everything will happen in a rush.
A few miles further upstream, the flood curve becomes even steeper and sometimes creates the famous Severn Bore.
Credit: Maxine Heath
Across the river from Sharpness, at Lydney’s historic gated harbour, the tidal regime demands particularly good seamanship, because the Severn is another long, shallow estuary where the tide moves inland as a wave.
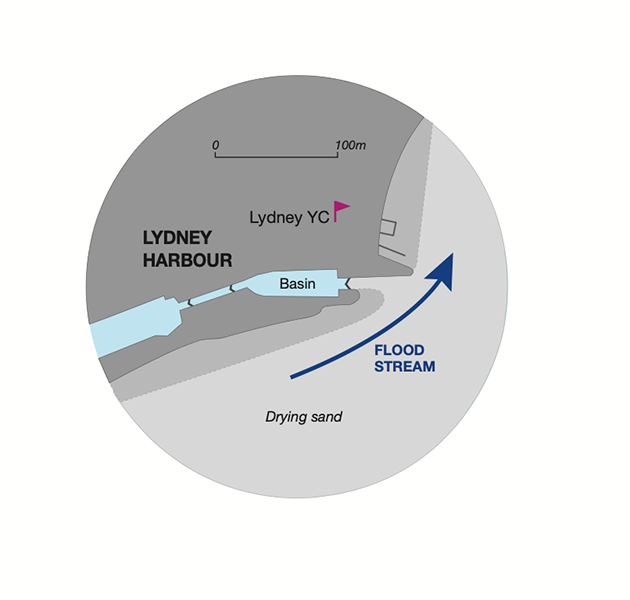
Credit: Maxine Heath
As in all waves, the water at the crest is surging forward and reversal of flow does not occur until some time after the crest has passed, when the water level is already dropping (see Diagram 7).
However, Lydney’s gates have to be shut before the tide begins to drop, to avoid damage to the primitive closing mechanism.
This means that an in-coming boat must enter no later than dead high water, when the flood tide will still be sluicing across the narrow harbour mouth – at possibly 4 knots.
In the old days, coasters would have been guided by local pilots and assisted into the dock by windlasses and warping sheaves.
The modern yacht skipper will probably have none of those aids but must rely on careful timing and faultless boat-handling. Tides do not merely rise and fall: the vertical movements are caused by horizontal flows and vice versa.

Lydney’s old harbour gates have to close before the tide begins to drop. Credit: Ken Endean
This should always be taken into account for pilotage within a shallow estuary, and it may be necessary to make adjustments to published data.
Wherever you are sailing, and whether or not you are nosing up shallow rivers or not, it pays to pay close attention to the shape of the tidal curve.
A perfect sine wave between single low-water and high-water points is in reality very rare.
Double high or low tides, long stands at either, and sudden changes in height are common all around the coast of our islands, and trusting what a web prediction churns out could land you aground.
Barnstaple – a caution
Barnstaple is featured in this article because its tidal patterns are interesting, and not because I am recommending a visit.
A passage up the River Taw will involve difficulties, including sand banks, strong currents, rock ledges, missing pole beacons and very few other navigation aids.
Then comes confusion at Barnstaple’s high-level Western Bypass Bridge.
Current charts have an adjacent note referring to a swing bridge with 1.8m headroom, but that is a different bridge, over the River Yeo tributary, and there is no air draught note for the high-level bridge.
It is reported to have a centre-span air draught of 12m above MHWS but there is a high sand bank under that span; the principal channel is under the north-of-centre span but there appears to be no air draught figure published for that span.
So take great care if you do visit or stay downstream!
Enjoyed reading Tidal calculations: why online predictions can be dangerously inaccurate?
A subscription to Yachting Monthly magazine costs around 40% less than the cover price.
Print and digital editions are available through Magazines Direct – where you can also find the latest deals.
YM is packed with information to help you get the most from your time on the water.
-
-
-
- Take your seamanship to the next level with tips, advice and skills from our experts
- Impartial in-depth reviews of the latest yachts and equipment
- Cruising guides to help you reach those dream destinations
-
-
Follow us on Facebook, Twitter and Instagram.
The post Tidal calculations: why online predictions can be dangerously inaccurate appeared first on Yachting Monthly.



